- github : https://github.com/skarupke/branchless_binary_search
- 원문 : https://probablydance.com/2023/04/27/beautiful-branchless-binary-search/
- 작성 :
Malte Skarupke - 번역 : https://j2doll.tistory.com/1166
저는 Alex Muscar의 블로그 게시물인 D에서의 아름다운 이진 탐색 을 읽었습니다.
그 게시물에는 "샤 알고리즘(Shar’s algorithm)"이라는 이진 탐색이 설명되어 있습니다.
저는 그것에 대해 들어본 적이 없었고 구글링도 불가능했지만, 그 알고리즘을 보고는 "이건 분기가 없는 거야(branchless)"라고 생각하지 않을 수 없었습니다.
그리고 분기가 없는 이진 탐색이 있을 수 있다는 걸 누가 알았을까요? 그래서 저는 그것을 C++ 반복자를 위한 알고리즘으로 변환하는 작업을 했고, 더 이상 1부터 시작하는 인덱싱이나 고정 크기 배열이 필요하지 않았습니다.
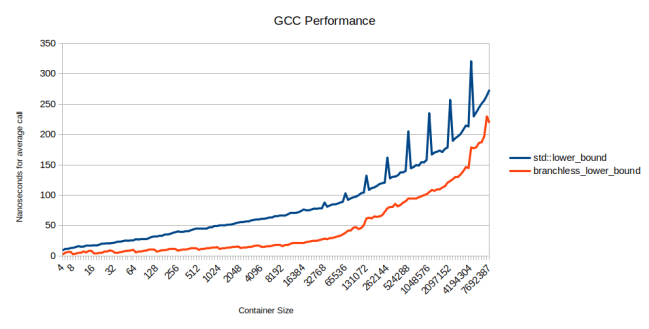
GCC에서는 std::lower_bound보다 두 배 이상 빠릅니다.
std::lower_bound는 이미 매우 고품질의 이진 검색입니다.
검색 루프는 간단하고 생성된 어셈블리는 아름답습니다.
이것이 존재하고 아무도 사용하지 않는 것 같다는 사실에 놀랐습니다…
코드 부터 시작해 보겠습니다
cpp
01: template<typename It, typename T, typename Cmp>
02: It branchless_lower_bound(It begin, It end, const T & value, Cmp && compare)
03: {
04: size_t length = end - begin;
05: if (length == 0)
06: return end;
07: size_t step = bit_floor(length);
08: if (step != length && compare(begin[step], value))
09: {
10: length -= step + 1;
11: if (length == 0)
12: return end;
13: step = bit_ceil(length);
14: begin = end - step;
15: }
16: for (step /= 2; step != 0; step /= 2)
17: {
18: if (compare(begin[step], value))
19: begin += step;
20: }
21: return begin + compare(*begin, value);
22: }
23: template<typename It, typename T>
24: It branchless_lower_bound(It begin, It end, const T & value)
25: {
26: return branchless_lower_bound(begin, end, value, std::less<>{});
27: }
검색 루프는 간단하다고 말했지만, 불행히도 4~15행의 설정은 그렇지 않습니다.
지금은 건너뛰겠습니다.
대부분의 작업은 16~20행의 루프에서 발생합니다.
루프가 분기가 없는 것처럼 보이지 않을 수도 있는데, 루프 본문에 루프 조건문과 if 문이 분명히 있기 때문입니다. 이 두 가지를 모두 옹호하겠습니다.
- if 문은 CMOV(조건부 이동) 명령어로 컴파일되므로 분기가 없습니다. 최소한 GCC는 이렇게 합니다. 아무리 영리하게 노력해도 Clang이 이것을 분기가 없게 만들 수 없었습니다. 그래서 영리하게 행동하지 않기로 했습니다. GCC에서는 그렇게 할 수 있으니까요. C++에서 CMOV를 직접 사용할 수만 있다면 좋았을 텐데요...
- 루프 조건은 분기이지만 배열의 길이에만 의존합니다. 따라서 매우 잘 예측할 수 있으며 걱정할 필요가 없습니다. 링크된 블로그 게시물은 루프를 완전히 풀어서 이 분기가 사라지게 하지만, 제 벤치마크에서 풀림은 실제로 더 느렸습니다. 함수 본문이 너무 커져서 인라인으로 처리할 수 없었기 때문입니다. 그래서 그대로 두었습니다.
그럼 이제 제목이 한 가지 가지가 없어졌고 다른 한 가지가 거의 자유로워서 원한다면 제거할 수 있다는 사실을 설명했는데, 실제로 이게 어떻게 작동할까요?
중요한 변수는 7번째 줄의 step 변수입니다. 2의 거듭제곱으로 점프할 것입니다. 배열이 64개 요소 길이라면 64, 32, 16, 8, 4, 2, 1이라는 값을 가질 것입니다. 입력 길이의 가장 가까운 더 작은 2의 거듭제곱으로 초기화됩니다. 따라서 입력이 22개 요소 길이라면 16이 됩니다. 제 컴파일러에는 새로운 std::bit_floor 함수가 없으므로 가장 가까운 2의 거듭제곱으로 반올림하는 함수를 직접 작성했습니다. C++20이 더 널리 지원되면 이것을 std::bit_floor 에 대한 호출로 바꿔야 합니다.
우리는 항상 2의 거듭제곱 크기의 단계를 수행하지만, 입력 길이가 2의 거듭제곱이 아니면 문제가 될 것입니다. 따라서 8~15번째 줄에서 중간이 검색 값보다 작은지 확인합니다. 그렇다면 마지막 요소를 검색합니다. 또는 구체적으로 설명하자면, 입력 길이가 22이고 해당 부울 값이 거짓이면 인덱스 0에서 15까지 처음 16개 요소를 검색합니다. 해당 조건이 참이면 인덱스 14에서 21까지 마지막 8개 요소를 검색합니다
input 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
line 8 compare 16
when false 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
when true 14 15 16 17 18 19 20 21
네, 이는 인덱스 14, 15, 16이 8번째 줄의 비교에서 이미 제외했음에도 불구하고 후반에 포함된다는 것을 의미하지만, 그게 멋진 루프를 갖는 데 드는 대가입니다. 2의 거듭제곱으로 반올림해야 합니다.
어떻게 수행하나요? GCC에서 엄청나게 빠릅니다.
배열에 16k개의 요소가 있는 경우, 실제로는 std::lower_bound보다 3배 빠릅니다. 나중에 캐시 효과가 지배적이기 시작하므로 축소된 분기 미스가 덜 중요합니다.
std::lower_bound의 스파이크는 2의 거듭제곱에서 발생하는데, 어떻게 보면 훨씬 더 느립니다. 조금 살펴봤지만 쉽게 설명할 수 있는 게 떠오르지 않습니다. Clang 버전은 매우 다른 어셈블리로 컴파일하더라도 같은 스파이크가 발생합니다.
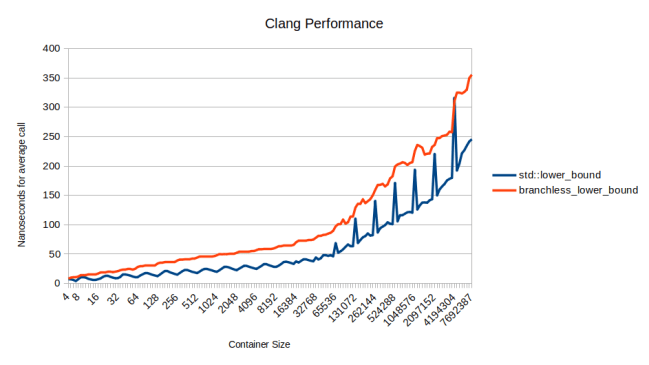
사실 Clang에서 branchless_lower_bound는 std::lower_bound보다 느립니다. 실제로 branchless로 만들 수 없었기 때문입니다.
재밌는 건 Clang이 std::lower_bound를 분기 없는 상태로 컴파일한다는 거예요. 그래서 std::lower_bound는 GCC보다 Clang에서 더 빠르고, 제 branchless_lower_bound는 분기 없는 상태가 아니에요. 빨간색 선이 위로 이동했을 뿐만 아니라 파란색 선도 아래로 이동했어요.
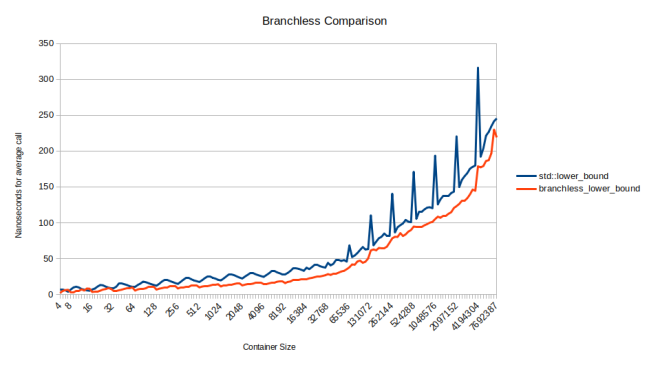
하지만 이는 std::lower_bound의 Clang 버전을 branchless_lower_bound의 GCC 버전과 비교하면 두 개의 branchless 알고리즘을 비교할 수 있다는 것을 의미합니다. 그렇게 해보겠습니다.
branchless_lower_bound의 branchless 버전은 std::lower_bound의 branchless 버전보다 빠릅니다. 배열이 더 작은 그래프의 왼쪽 절반에서는 평균적으로 1.5배 빠릅니다. 이유는? 주로 내부 루프가 너무 좁기 때문입니다. 다음은 두 가지에 대한 어셈블리입니다
| inner loop of std::lower_bound | inner loop of branchless_lower_bound |
|---|---|
| loop: mov %rcx,%rsi | loop: lea (%rdx,%rax,4),%rcx |
| mov %rbx,%rdx | cmp (%rcx),%esi |
| shr %rdx | cmovg %rcx,%rdx |
| mov %rdx,%rdi | shr %rax |
| not %rdi | jne loop |
| add %rbx,%rdi | |
| cmp %eax,(%rcx,%rdx,4) | |
| lea 0x4(%rcx,%rdx,4),%rcx | |
| cmovge %rsi,%rcx | |
| cmovge %rdx,%rdi | |
| mov %rdi,%rbx | |
| test %rdi,%rdi | |
| jg loop |
이것들은 모두 명령어 수준 병렬성이 약간만 있는 매우 저렴한 연산입니다(각 루프 반복은 이전 반복에 따라 달라지므로 이 두 가지 모두에 대해 클럭당 명령어가 낮습니다). 따라서 이를 세는 것만으로 비용을 추정할 수 있습니다. 13 대 5는 큰 감소입니다. 구체적으로 두 가지 차이점이 중요합니다.
- branchless_lower_bound는 두 개의 포인터 대신 하나의 포인터만 추적하면 됩니다.
- std::lower_bound는 각 반복 후에 크기를 다시 계산해야 합니다. branchless_lower_bound에서 다음 반복의 크기는 이전 반복에 따라 달라지지 않습니다.
이건 훌륭하지만, 비교 함수는 사용자가 제공하고, 훨씬 더 큰 경우 우리보다 훨씬 더 많은 사이클이 걸릴 수 있습니다. 그런 경우 branchless_lower_bound는 std::lower_bound보다 느릴 것입니다. 다음은 문자열의 이진 검색으로, 컨테이너가 커지면 비용이 더 많이 듭니다.
문자열에 대해 왜 더 느린가요? std::lower_bound보다 더 많은 비교를 하기 때문입니다. 2의 거듭제곱으로 나누는 것은 실제로 이상적이지 않습니다. 예를 들어 입력이 배열 [0, 1, 2, 3, 4]이고 가운데, 요소 2를 찾고 있다면 이것은 매우 나쁘게 동작합니다.
| std::lower_bound | branchless_lower_bound |
|---|---|
| compare at index 2, not less | compare at index 4, not less |
| compare at index 1, less | compare at index 2, not less |
| done, found at index 2 | compare at index 1, less |
| compare at index 1, less | |
| done, found at index 2 |
그래서 우리는 std::lower_bound가 두 개만 필요로 하는 네 개의 비교를 여기서 하고 있습니다. 저는 특히 어색한 예를 하나 골랐는데, 중앙에서 멀리 떨어진 곳에서 시작하여 같은 인덱스를 두 번 비교합니다. 여러분이 이걸 정리할 수 있을 것 같지만, 제가 시도했을 때 항상 더 느리게 만들었습니다.
하지만 이상적인 이진 탐색보다 2^n 요소 보다 작은 배열의 경우 훨씬 더 나쁘지는 않을 겁니다.
- 이상적인 이진 탐색은 n 또는 그보다 적은 비교를 사용할 것입니다.
- branchless_lower_bound는 (n+1) 또는 그보다 적은 비교를 사용할 것입니다.
전반적으로 가치가 있습니다. 반복 횟수가 더 많지만, 그 추가 반복 횟수를 훨씬 더 빨리 처리하기 때문에 결국에는 훨씬 더 빠르게 나옵니다. 비교 함수가 비용이 많이 든다면 std::lower_bound가 더 나은 선택일 수 있다는 점을 명심해야 합니다.
저는 처음에 "샤의 알고리즘"은 구글링이 불가능하다고 말했습니다. 알렉스 무스카는 존 L 벤틀리가 1982년에 쓴 책에서 읽었다고 말했습니다. 다행히도 그 책은 인터넷 아카이브에서 온라인으로 빌릴 수 있습니다. 벤틀리는 소스 코드를 제공하고 Knuth의 "Sorting and Searching"에서 아이디어를 얻었다고 말합니다. Knuth는 소스 코드를 제공하지 않았습니다. 그는 자신의 책에서 그 아이디어를 간략하게 설명했을 뿐이며, 1971년 레너드 E 샤가 그 아이디어를 얻었다고 말합니다. 샤가 그 아이디어를 어디서 썼는지는 모르겠습니다. 아마 그는 Knuth에게 말했을 겁니다.
이것은 제가 Knuth의 책에서 뛰어나고 더 널리 사용되어야 할 알고리즘을 발견한 두 번째 이지만 어떻게 된 일인지 잊혀졌습니다. 아마도 실제로 책을 읽어야 할 것입니다... 어떤 아이디어가 좋고 어떤 아이디어가 좋지 않은지 알아내기가 정말 어렵습니다. 예를 들어 Shar의 알고리즘을 스케치한 직후 Knuth는 피보나치 수열을 기반으로 한 이진 검색을 검토하는 데 훨씬 더 많은 시간을 보냅니다. 정수를 2로 빠르게 나눌 수 없고 대신 덧셈과 뺄셈만 있는 경우 더 빠릅니다. 따라서 쓸모가 없을 가능성이 높지만 누가 알겠습니까? Knuth의 책을 읽을 때 대부분 알고리즘은 쓸모가 없고 좋은 점은 이미 누군가 강조했을 것이라고 가정해야 합니다. 다행히 저와 같은 사람들에게는 여전히 몇 가지 숨겨진 보석이 있는 것 같습니다.
이 코드는 여기 에서 사용할 수 있습니다. Boost 라이선스에 따라 출시되었습니다.
또한 기부 버튼을 시도하고 있습니다. 이와 같은 오픈소스 작업이 귀하에게 가치 있다면 비용을 지불하는 것을 고려하세요. 권장 기부금은 개인의 경우 20달러(또는 레스토랑 메뉴에 있는 품목에 대한 현지 비용)이고, 조직의 경우 1000달러(또는 하루 동안 계약자를 고용하는 현지 비용)입니다. 그러나 어떤 금액이든 환영합니다.
'C C++' 카테고리의 다른 글
| C++에서 다국어 문자 타입의 발전: char8_t, char16_t, char32_t (0) | 2025.02.18 |
|---|---|
| utf8.h : C와 C++에 대한 단일 헤더(header) utf8 문자열 함수 (0) | 2025.02.18 |
| C++ std::swap() 와 std::move() 의 작동 방식과 내부 원리 (0) | 2025.02.13 |
| noexcept in Modern C++ (0) | 2025.02.13 |
| C++17 std::is_base_of_v 사용법 및 예제 (0) | 2025.02.12 |